Skip list
| Part of a series on |
| Probabilistic data structures |
|---|
| Bloom filter · Skip list |
| Random trees |
| Rapidly-exploring random tree |
| Related |
| Randomized algorithm |
| Computer science Portal |
A skip list is a data structure for storing a sorted list of items using a hierarchy of linked lists that connect increasingly sparse subsequences of the items. These auxiliary lists allow item lookup with efficiency comparable to balanced binary search trees (that is, with number of probes proportional to log n instead of n).
Each link of the sparser lists skips over many items of the full list in one step, hence the structure's name. These forward links may be added in a randomized way with a geometric / negative binomial distribution.[1] Insert, search and delete operations are performed in logarithmic expected time. The links may also be added in a non-probabilistic way so as to guarantee amortized (rather than merely expected) logarithmic cost.
Contents |
Description
A skip list is built in layers. The bottom layer is an ordinary ordered linked list. Each higher layer acts as an "express lane" for the lists below, where an element in layer i appears in layer i+1 with some fixed probability p (two commonly-used values for p are 1/2 or 1/4). On average, each element appears in 1/(1-p) lists, and the tallest element (usually a special head element at the front of the skip list) in 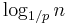 lists.
lists.
A search for a target element begins at the head element in the top list, and proceeds horizontally until the current element is greater than or equal to the target. If the current element is equal to the target, it has been found. If the current element is greater than the target, or the search reaches the end of the linked list, the procedure is repeated after returning to the previous element and dropping down vertically to the next lower list. The expected number of steps in each linked list is at most 1/p, which can be seen by tracing the search path backwards from the target until reaching an element that appears in the next higher list or reaching the beginning of the current list. Therefore, the total expected cost of a search is 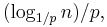 which is
which is 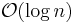 when p is a constant. By choosing different values of p, it is possible to trade search costs against storage costs.
when p is a constant. By choosing different values of p, it is possible to trade search costs against storage costs.
Implementation details
The elements used for a skip list can contain more than one pointer since they can participate in more than one list.
Insertions and deletions are implemented much like the corresponding linked-list operations, except that "tall" elements must be inserted into or deleted from more than one linked list.
Θ(n) operations, which force us to visit every node in ascending order (such as printing the entire list), provide the opportunity to perform a behind-the-scenes derandomization of the level structure of the skip-list in an optimal way, bringing the skip list to 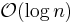 search time. (Choose the level of the i'th finite node to be 1 plus the number of times we can repeatedly divide i by 2 before it becomes odd. Also, i=0 for the negative infinity header as we have the usual special case of choosing the highest possible level for negative and/or positive infinite nodes.) However this also allows someone to know where all of the higher-than-level 1 nodes are and delete them.
search time. (Choose the level of the i'th finite node to be 1 plus the number of times we can repeatedly divide i by 2 before it becomes odd. Also, i=0 for the negative infinity header as we have the usual special case of choosing the highest possible level for negative and/or positive infinite nodes.) However this also allows someone to know where all of the higher-than-level 1 nodes are and delete them.
Alternatively, we could make the level structure quasi-random in the following way:
make all nodes level 1
j ← 1
while the number of nodes at level j > 1 do
for each i'th node at level j do
if i is odd
if i is not the last node at level j
randomly choose whether to promote it to level j+1
else
do not promote
end if
else if i is even and node i-1 was not promoted
promote it to level j+1
end if
repeat
j ← j + 1
repeat
Like the derandomized version, quasi-randomization is only done when there is some other reason to be running a Θ(n) operation (which visits every node).
The advantage of this quasi-randomness is that it doesn't give away nearly as much level-structure related information to an adversarial user as the de-randomized one. This is desirable because an adversarial user who is able to tell which nodes are not at the lowest level can pessimize performance by simply deleting higher-level nodes. The search performance is still guaranteed to be logarithmic.
It would be tempting to make the following "optimization": In the part which says "Next, for each i'th...", forget about doing a coin-flip for each even-odd pair. Just flip a coin once to decide whether to promote only the even ones or only the odd ones. Instead of Θ(n lg n) coin flips, there would only be Θ(lg n) of them. Unfortunately, this gives the adversarial user a 50/50 chance of being correct upon guessing that all of the even numbered nodes (among the ones at level 1 or higher) are higher than level one. This is despite the property that he has a very low probability of guessing that a particular node is at level N for some integer N.
The following proves these two claims concerning the advantages of quasi-randomness over the totally derandomized version. First, to prove that the search time is guaranteed to be logarithmic. Suppose a node n is searched for, where n is the position of the found node among the nodes of level 1 or higher. If n is even, then there is a 50/50 chance that it is higher than level 1. However, if it is not higher than level 1 then node n-1 is guaranteed to be higher than level 1. If n is odd, then there is a 50/50 chance that it is higher than level 1. Suppose that it is not; there is a 50/50 chance that node n-1 is higher than level 1. Suppose that this is not either; we are guaranteed that node n-2 is higher than level 1. The analysis can then be repeated for nodes of level 2 or higher, level 3 or higher, etc. always keeping in mind that n is the position of the node among the ones of level k or higher for integer k. So the search time is constant in the best case (if the found node is the highest possible level) and 2 times the worst case for the search time for the totally derandomized skip-list (because we have to keep moving left twice rather than keep moving left once).
Next, an examination of the probability of an adversarial user's guess of a node being level k or higher being correct. First, the adversarial user has a 50/50 chance of correctly guessing that a particular node is level 2 or higher. This event is independent of whether or not the user correctly guesses at some other node being level 2 or higher. If the user knows the positions of two consecutive nodes of level 2 or higher, and knows that the one on the left is in an odd numbered position among the nodes of level 2 or higher, the user has a 50/50 chance of correctly guessing which one is of level 3 or higher. So, the user's probability of being correct, when guessing that a node is level 3 or higher, is 1/4. Inductively continuing this analysis, we see that the user's probability of guessing that a particular node is level k or higher is 1/(2^(k-1)).
The above analyses only work when the number of nodes is a power of two. However, because of the third rule which says, "Finally, if i is odd and also the last node at level 1 then do not promote." (where we substitute the appropriate level number for 1) it becomes a sequence of exact-power-of-two-sized skiplists, concatenated onto each other, for which the analysis does work. In fact, the exact powers of two correspond to the binary representation for the number of nodes in the whole list.
A skip list, upon which we have not recently performed either of the above mentioned Θ(n) operations, does not provide the same absolute worst-case performance guarantees as more traditional balanced tree data structures, because it is always possible (though with very low probability) that the coin-flips used to build the skip list will produce a badly balanced structure. However, they work well in practice, and the randomized balancing scheme has been argued to be easier to implement than the deterministic balancing schemes used in balanced binary search trees. Skip lists are also useful in parallel computing, where insertions can be done in different parts of the skip list in parallel without any global rebalancing of the data structure. Such parallelism can be especially advantageous for resource discovery in an ad-hoc Wireless network because a randomized skip list can be made robust to the loss of any single node.[2]
There has been some evidence that skip lists have worse real-world performance and space requirements than B trees due to memory locality and other issues.[3]
Indexable skiplist
As described above, a skiplist is capable of fast Θ(log n) insertion and removal of values from a sorted sequence, but it has only slow Θ(n) lookups of values at a given position in the sequence (i.e. return the 500th value); however, with a minor modification the speed of random access indexed lookups can be improved to Θ(log n).
For every link, also store the width of the link. The width is defined as the number of bottom layer links being traversed by each of the higher layer "express lane" links.
For example, here are the widths of the links in the example at the top of the page:
1 10
o-----> o-----------------------------------------------------------------------------> o TOP LEVEL
1 3 2 5
o-----> o---------------------> o-------------> o-------------------------------------> o LEVEL 3
1 2 1 2 5
o-----> o-------------> o-----> o-------------> o-------------------------------------> o LEVEL 2
1 1 1 1 1 1 1 1 1 1 1
o-----> o-----> o-----> o-----> o-----> o-----> o-----> o-----> o-----> o-----> o-----> o BOTTOM LEVEL
Head Node1 Node2 Node3 Node4 Node5 Node6 Node7 Node8 Node9 Node10 NIL
Notice that the width of a higher level link is the sum of the component links below it (i.e. the width 10 link spans the links of widths 3, 2 and 5 immediately below it). Consequently, the sum of all widths is the same on every level (10 + 1 = 1 + 3 + 2 + 5 = 1 + 2 + 1 + 2 + 5).
To index the skiplist and find the i-th value, traverse the skiplist while counting down the widths of each traversed link. Descend a level whenever the upcoming width would be too large.
For example, to find the node in the fifth position (Node 5), traverse a link of width 1 at the top level. Now four more steps are needed but the next width on this level is ten which is too large, so drop one level. Traverse one link of width 3. Since another step of width 2 would be too far, drop down to the bottom level. Now traverse the final link of width 1 to reach the target running total of 5 (1+3+1).
function lookupByPositionIndex(i)
node ← head
i ← i + 1 # don't count the head as a step
for level from top to bottom do
while i ≥ node.width[level] do # if next step is not too far
i ← i - node.width[level] # subtract the current width
node ← node.next[level] # traverse forward at the current level
repeat
repeat
return node.value
end function
This method of implementing indexing is detailed in Section 3.4 Linear List Operations in "A skip list cookbook" by William Pugh.
Also, see Running Median using an Indexable Skiplist for a complete implementation written in Python and for an example of it being used to solve a computationally intensive statistics problem. And see Regaining Lost Knowledge for the history of that solution.
History
Skip lists were first described in 1990 by William Pugh. He details how they work in Skip lists: a probabilistic alternative to balanced trees in Communications of the ACM, June 1990, 33(6) 668-676. See also citations and downloadable documents.
To quote the author:
- Skip lists are a probabilistic data structure that seem likely to supplant balanced trees as the implementation method of choice for many applications. Skip list algorithms have the same asymptotic expected time bounds as balanced trees and are simpler, faster and use less space.
Usages
List of applications and frameworks that use skip lists:
- QMap template class of Qt that provides a dictionary.
- Redis is an ANSI-C open-source persistent key/value store for Posix systems, uses skip lists in its implementation of ordered sets.
- skipdb is an open-source database format using ordered key/value pairs.
- Running Median using an Indexable Skiplist is a Python implementation of a skiplist augmented by link widths to make the structure indexable (giving fast access to the nth item). The indexable skiplist is used to efficiently solve the running median problem (recomputing medians and quartiles as values are added and removed from a large sliding window).
- ConcurrentSkipListSet and ConcurrentSkipListMap in the Java 1.6 API.
Skip lists are also used in distributed applications (where the nodes represent physical computers, and pointers represent network connections) and for implementing highly scalable concurrent priority queues with less lock contention,[4] or even without locking,[5][6][7] as well lockless concurrent dictionaries.[8] There are also several US patents for using skip lists to implement (lockless) priority queues and concurrent dictionaries.
References
- ^ Pugh, William (June 1990). "Skip lists: a probabilistic alternative to balanced trees". Communications of the ACM 33 (6): 668–676. doi:10.1145/78973.78977.
- ^ Shah, Gauri Ph.D.; James Aspnes (December 2003) (PDF). Distributed Data Structures for Peer-to-Peer Systems. http://www.cs.yale.edu/homes/shah/pubs/thesis.pdf. Retrieved 2008-09-23.
- ^ http://resnet.uoregon.edu/~gurney_j/jmpc/skiplist.html
- ^ Skiplist-based concurrent priority queues
- ^ Sundell, H.; Tsigas, P. (2003). "Fast and lock-free concurrent priority queues for multi-thread systems". Proceedings International Parallel and Distributed Processing Symposium. pp. 11. doi:10.1109/IPDPS.2003.1213189. ISBN 0-7695-1926-1.
- ^ Fomitchev, M.; Ruppert, E. (2004). "Lock-free linked lists and skip lists". Proceedings of the twenty-third annual ACM symposium on Principles of distributed computing - PODC '04. pp. 50. doi:10.1145/1011767.1011776. ISBN 1581138024.
- ^ Bajpai, R.; Dhara, K. K.; Krishnaswamy, V. (2008). "QPID: A Distributed Priority Queue with Item Locality". 2008 IEEE International Symposium on Parallel and Distributed Processing with Applications. pp. 215. doi:10.1109/ISPA.2008.90. ISBN 978-0-7695-3471-8.
- ^ Sundell, H. K.; Tsigas, P. (2004). "Scalable and lock-free concurrent dictionaries". Proceedings of the 2004 ACM symposium on Applied computing - SAC '04. pp. 1438. doi:10.1145/967900.968188. ISBN 1581138121.
External links
- Skip Lists: A Probabilistic Alternative to Balanced Trees - William Pugh's original paper
- "Skip list" entry in the Dictionary of Algorithms and Data Structures
- Skip Lists: A Linked List with Self-Balancing BST-Like Properties on MSDN in C# 2.0
- SkipDB, a BerkeleyDB-style database implemented using skip lists.
- Skip Lists lecture (MIT OpenCourseWare: Introduction to Algorithm)
- Demo applets
- Skip List Applet by Kubo Kovac
- Thomas Wenger's demo applet on skiplists
- Implementations